
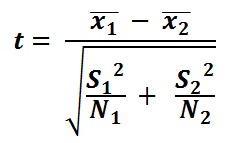
You calculate the mean by adding up all the data points in the group and then dividing the total by the number of data points. Mean: The mean is the average value in a data set. The key features of the normal distribution are the mean, or average value, and the variance, or how widely the data is spread around the mean. Using an agricultural example, if you recorded the average corn yield from all the farmers in a given area, those yields would probably follow a normal distribution.

This phenomenon occurs regularly in nature and is the basis for the statistics we use in on-farm research. The data in a normal distribution is often described as following a bell-shaped curve (Figure 7). Normal distribution: The normal distribution describes a collection of data organized around an average value (the mean), with greater or lesser data points distributed approximately equally on either side of that value. Before we get into the specifics of those techniques, here is a review of some basic statistics terminology: In most situations, you will also want to consult with your agricultural advisor or Cooperative Extension personnel for guidance and assistance with your data analysis.
#Statistics practice basic statistical calculations software#
You can learn to do your own data analysis either by hand or using a statistical software program. The two types of statistical analysis covered here are the t-test and ANOVA. Recall that the type of statistics you use to analyze your data follows directly from your experimental design (Table 2). This section looks at statistical analysis in more detail, expanding on step 9 in the process outlined earlier. Statistical analysis involves a sequence of mathematical computations for comparing treatments and evaluating whether any observed differences are truly a result of the change in practices, or if the differences may be due to chance and natural variation.


 0 kommentar(er)
0 kommentar(er)
